[旧作汇集]小波学习之三(多孔算法与MATLAB swt剖析)
纠错
11 May 2016
原始版本在CSDN博客上发表, 发表于 2013-05-24 17:54 小波学习之三(多孔算法与MATLAB swt剖析)
一、多孔算法原理介绍
多孔算法(a trous algorithm)是由M.Shen于1992年提出的一种利用Mallat算法结构计算小波变换的快速算法,因在低通滤波器h0(k)和高通滤波器h1(k)中插入适当数目的零点而得名。它适用于a=2j的二分树结构,与Mallat算法的电路实现结构相似。
比较详细的介绍如下,来自论文《基于小波多孔变换的多传感器多目标跟踪航迹关联算法研究》http://www.docin.com/p-143869263.html。


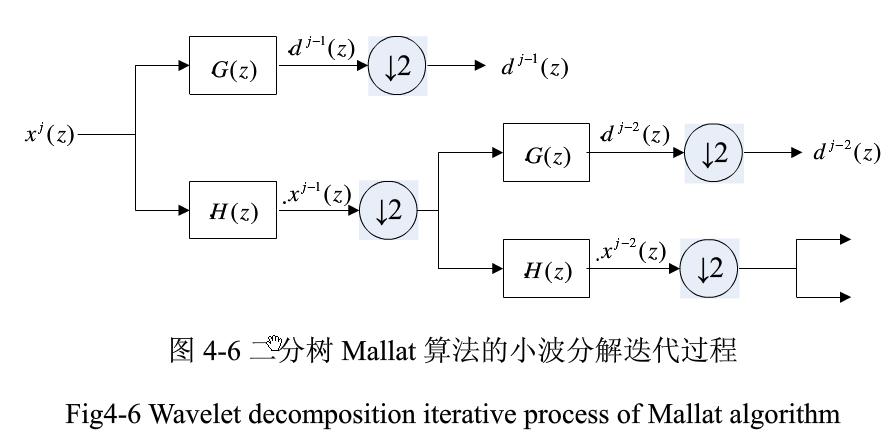
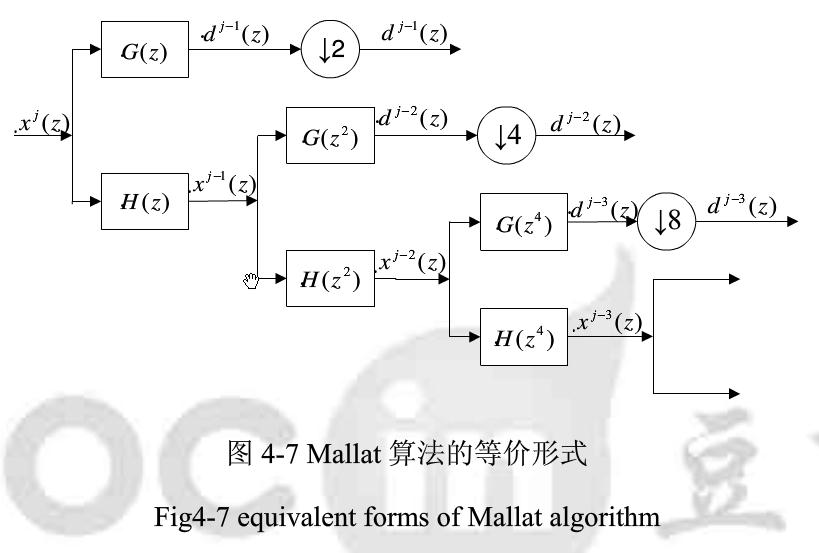
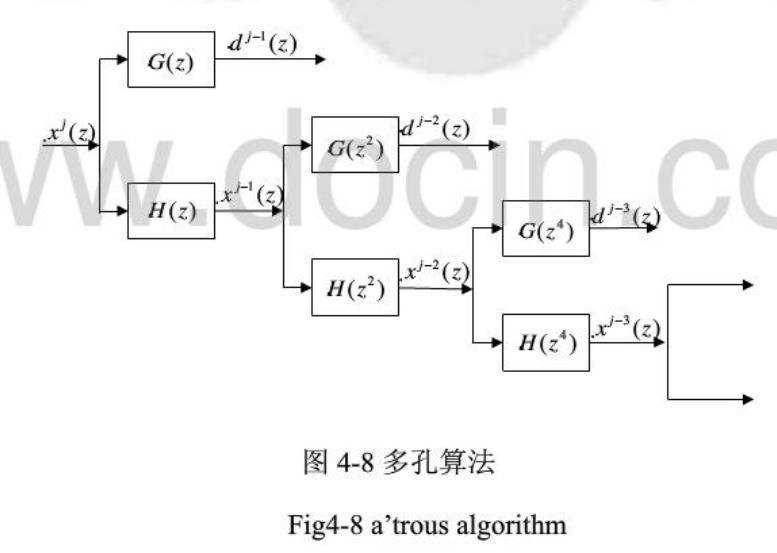

二、多孔算法经验之谈
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | 通过学习小波变换的多孔算法,发现很难理解,很多东西似懂非懂,比较困惑。下面的经验之谈来自网络,可以帮助理解。(http://www.360doc.com/content/10/0729/17/42159_42312820.shtml)
“小波的问题在那里?其中之一,平移不变性。说白了,先将源信号平移n位,再做小波变换,和先将源信号做小波变换,再平移n位,结果不同。这对于实时处理和一些场合是极为不便的。(gibbs效应于此也有关)。
怎么办?多孔算法(a trous)可以解决此瓶颈。多孔算法,又称非抽取小波变换,即undecimated wavelet transform or nonsampled wavelet transform,简写(NSWT)。(有可能二进小波变换也是一个意思)。
实现多孔算法,需要什么呢?回答MALLAT算法是基础。若你不懂MALLAT,请去学习,或看我置顶的贴子。我可以告诉大家,我写TROUS代码从看论文到完成只用了10分钟。
但单单MALLAT算法够吗?答案否定的。我们必须找到两种算法的不同点。方可得心应手。这里我浅谈一二。
首先,为什么MALLAT不具有移不变特点而TROUS具有移不变特点。根源就在抽取插值上。看这个系统Y(N)=X(2N),它是不是移不变系统,显然不是。现在大家明白了吧。所以非抽取算法,是移不变的。而这个移不变所付出的代价,就是高频分量加低频分量长度再不是源信号的长度,而是源信号长度的2倍。
其次,滤波器还是可以用,WFILTERS()。而且重构和分解滤波器的关系,还是逆序后再右移一位(圆周卷积+周期延托)。但所有的滤波器系数要乘以SQRT(2)/2。为什么,答案在PR条件上。MALLET算法PR条件有两个,一个是抗混叠,另一个是完全重构。而多孔算法由于非插值抽取,只有完全重构,且等式的右边常数是“1”,而不是MALLET-PR条件的“2”。所以MALLET的PR条件要乘以“1/2”才和TROUS一致,而这个因子“1/2”正好被分配到两个滤波器上,所以是SQRT(2)/2。
再次,在每一层的下一层,滤波器中间要插值0。为什么?从谱上看,这是小波最经典的物理意义。数字信号一个周期的频谱范围为[-PI PI],MALLAT算法的低通滤波[-PI/2 PI/2],高通滤波[-PI -PI/2] U [PI/2 PI],则滤波后低频分量频谱范围[-PI/2 PI/2]。这时注意“开始抽取,频谱展宽”,又回到源信号频谱[-PI PI],然后再低通、高通滤波,周而复始。(小波包的问题顺便也说一下,实际上将高频抽取,频谱展宽后,发生了频谱颠倒现象,论坛里对此有精彩讨论,对此不再赘述。)而多孔呢?情况变了。低频分量始终是[-PI/2 PI/2],若低通滤波器仍是[-PI/2 PI/2],高通滤波器[-PI -PI/2] U [PI/2 PI],岂不是有些可笑吗?于是“滤波器插值”极其精妙的登场。低通和高通滤波器频谱变窄,低通[-PI/4 PI/4],高通[-PI/2 -PI/4] U [PI/4 PI/2],这下物理概念对了。那多孔有没有小波包呢,留给大家探讨。”
|
三、多孔算法MATLAB实现解析
1 | MATLAB小波工具箱中的swt/iswt在离散化实现时本质上采用了多孔算法,但有些差别,主要体现在滤波器的操作上,严格的多孔算法在mallat滤波器上乘以sqrt(2)/2,而swt/iswt没有这样处理。其他差别待后续用MATLAB实现严格多孔算法后,再对比给出。 |
【——2013.5.27有更新
讨论:关于滤波器乘以sqrt(2)/2是否为多孔算法的必要条件,目前网上还存在争议。第一种观点认为“A trous 算法与SWT不一样,主要体现在滤波器的操作上,前者体现在滤波器乘以sqrt(2)/2,后者没有,不过两种算法都有滤波器插零的操作”。第二种观点认为“SWT在离散化实现时采用了a-trous算法”,即有无sqrt(2)/2并无本质区别,都是多孔算法。
刚开始以为观点一有道理,目前逐渐倾向于观点二。到底如何,待进一步熟悉理解,目前仅供讨论。
观点一来源:http://blog.csdn.net/windydreams/article/details/8063093
观点二来源:http://www.ilovematlab.cn/thread-102623-1-1.html】
接下来分析一下MATLAB swt的实现算法。
1 | MATLAB中swt实现算法示意图 |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | MATLAB中swt实现过程主要步骤是:
假设x=[x(1) x(2) x(3) x(4) x(5) x(6) x(7)],计算[swa, swd] = swt(x,1,’db2’),其计算过程主要由以下几部分组成:
1、边缘延拓,由函数wextend完成。
仔细分析子程序部分,函数wextend的用法为x=wextend('1D','per',x,length(lo)/2),其中lo为滤波器,length(lo_db2)/2=2,则这样得到的x=[x(6) x(7) x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(1) x(2)]。
2、卷积运算,由函数wconv1完成。
低频系数:
a=wconv1(x,lo),相当于a=conv2(x,lo,'full'),conv2的详细说明见dwt的解释。
a=[a(1) a(2) a(3) a(4) a(5) a(6) a(7) a(8) a(9) a(10) a(11) a(12) a(13) a(14)]
高频系数:
d=wconv1(x,hi),相当于d=conv2(x,hi,'full'),conv2的详细说明见dwt的解释。
d=[d(1) d(2) d(3) d(4) d(5) d(6) d(7) d(8) d(9) d(10) d(11) d(12) d(13) d(14)]
3、抽取分解结果,由函数wkeep1完成。
swa(1,:) = wkeep1(a,7,5) = [a(5) a(6) a(7) a(8) a(9) a(10) a(11)]
swd(1,:) = wkeep1(d,7,5) = [d(5) d(6) d(7) d(8) d(9) d(10) d(11)]
至此,1级swt分解完成,然后输出[swa, swd]结果。
假如进行多级swt分解,则继续下一步。
4、滤波器隔点插0,由dyadup实现。
lo = dyadup(lo,evenoddVal,evenLEN) = dyadup(lo,0,1) = [l(1) 0 l(2) 0 l(3) 0 l(4) 0];
hi = dyadup(hi,evenoddVal,evenLEN) = dyadup(hi,0,1) = [h(1) 0 h(2) 0 h(3) 0 h(4) 0];
然后,以上一级的swa作为信号,重复步骤1、2、3则得到第2级swt分解。同理,循环上述步骤可以得到3、4、5。。。i 级swt分解结果。
|
1 | 综上所述,swt与dwt的主要差别在于,1)增加了步骤4对滤波器隔点插0;2)抽取分解结果时,swt抽取的长度与原始信号长度一样,而dwt则抽取了原始信号长度的(1/2)^i,在此i为level分解级数或分解层数。(个人理解,欢迎讨论交流) |