[旧作汇集]小波学习之二(单层一维离散小波变换DWT的Mallat算法C++实现优化)
纠错
11 May 2016
原始版本在CSDN博客上发表, 发表于 2013-03-30 15:43 小波学习之二(单层一维离散小波变换DWT的Mallat算法C++实现优化)
在上回《小波学习之一》中,已经详细介绍了Mallat算法C++实现,效果还可以,但也存在一些问题,比如,代码难于理解,同时出现了边界问题。在此,本文将重构代码,采用新的方法解决这些问题,同时也加深对小波变换的理解。
MATLAB作为经典的数学工具,分析其小波变换dwt和idwt实现后发现真的很经典,学习参考价值很高。下面结合南京理工大学 谭彩铭的《解读matlab之小波库函数》及MATLAB小波工具包中m文件的情况,作一个小结,最后用C++函数进行实现,并且编译调试OK。
一、MATLAB上dwt函数的工作过程
假设x=[x(1) x(2) x(3) x(4) x(5) x(6) x(7)],计算y=dwt(x,’db2’),其计算过程主要由三个部分组成: 1、边缘延拓,它主要由函数wextend完成。
仔细分析子程序部分,函数wextend的用法为y=wextend(‘1D’,’sym’,x,3);这样得到的y=[ x(3) x(2) x(1) x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(7) x(6) x(5)] 2、卷积运算,它主要由函数conv2完成。 仔细分析子程序部分,核心语句有z=conv2(y,Lo_D,’valid’);这里设Lo_D=[h(1) h(2) h(3) h(4)]。
这2步的实现过程示意图如下:
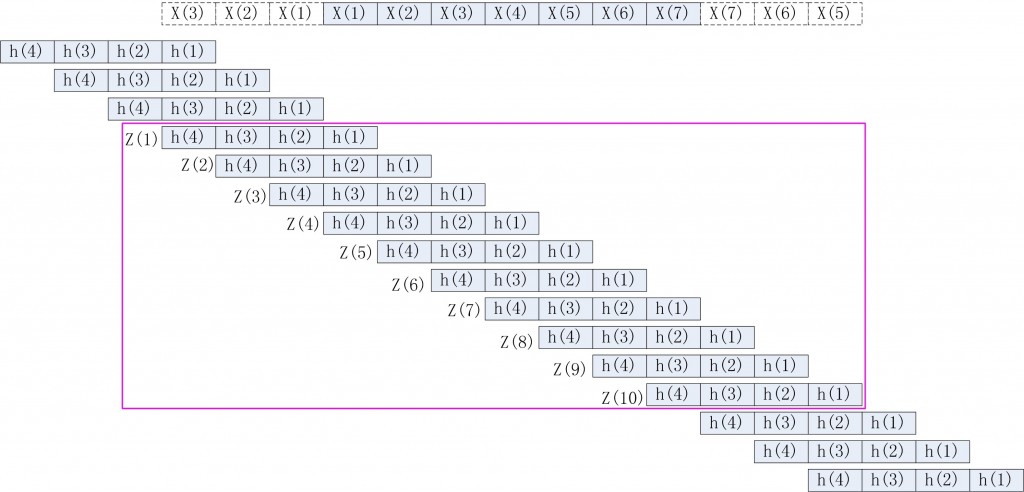
3、最后就是下采样即隔点采样,其下采样是按照式a = z(2:2:length(z))进行的,高频低频部分均如此,项数为floor((7+4-1)/2)。 最后的dwt低频系数结果是[z(2) z(4) z(6) z(8) z(10)],高频系数求解过程和低频系数一样,在此不再赘述。
二、MATLAB上idwt函数的工作过程
1、上采样即隔点插0,dyadup(x,0)。
2、卷积运算,它也是最终由函数conv2完成。
3、抽取结果,wkeep1(x,s,’c’)。
下面啥都不说show核心代码实现,欢迎讨论。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 | /**
* @brief 边缘延拓
* @param typeId 延拓数据的类型,1D or 2D
* @param modeId 延拓方式:对称、周期
* @param in 输入数据
* @param inLen 输入数据的长度
* @param filterLen 小波基滤波器长度
* @param out 返回结果数组
* @return 返回结果数组长度
*/
int SignalExtension(int typeId,
int modeId,
double *in,
int inLen,
int filterLen,
double out[])
{
if((NULL == in)||(NULL == out))
return -1;
if(0 != typeId) // 目前只支持一种模型
return -1;
//if(0 != modeId) // 目前只支持一种模型,信号对称拓延 'sym' or 'symh' Symmetric-padding (half-point): boundary value symmetric replication
// return -1;
if( inLen < filterLen ) // inLen should lager than or equal extendLen, otherwise no extension
return -1;
int i;
int extendLen = filterLen - 1;
if(0 == modeId) // 信号对称拓延
{
for(i=0; i<inLen; i++)
{
out[extendLen+i] = in[i];
}
for(i=0; i<extendLen; i++)
{
out[i] = out[2*extendLen - i - 1]; // 左边沿对称延拓
out[inLen + extendLen + i] = out[extendLen + inLen - i - 1]; // 右边沿对称延拓
}
return inLen + 2*extendLen;
}
else if(1 == modeId) // 信号周期拓延
{
for( i = 0; i < extendLen; i++ )
out[i] = in[inLen-extendLen+i];
for ( i = 0; i < inLen; i++ )
out[extendLen+i] = in[i];
return inLen + extendLen;
}
}
/**
* @brief 上采样 隔点插0
* @param data 输入数据指针
* @param n 输入数据长度
* @param result 返回结果数组
* @return 返回结果数组长度
*/
int Upsampling(double* data, int n, double result[])
{
int i;
for( i = 0; i < n; i++ )
{
result[2*i] = data[i];
result[2*i+1] = 0;
}
return( 2*n );
}
/**
* @brief 下采样 隔点采样
* @param data 输入数据指针
* @param n 输入数据长度
* @param result 返回结果数组
* @return 返回结果数组长度
*/
int Downsampling(double* data, int n, double result[])
{
int i, m;
m = n/2;
for( i = 0; i < m; i++ )
result[i] = data[i*2 + 1];
return( m );
}
/**
* @brief 卷积运算
* @param shapeId 卷积结果处理方式
* @param double *inSignal, int signalLen, // 输入信号及其长度
* @param double *inFilter, int filterLen, // 输入滤波器及其长度
* @param double outConv[], int *convLen) // 输出卷积结果及其长度
* @return
*/
void Conv1(int shapeId, // 卷积结果处理方式
double *inSignal, int signalLen, // 输入信号及其长度
double *inFilter, int filterLen, // 输入滤波器及其长度
double outConv[], int *convLen) // 输出卷积结果及其长度
{
if((NULL == inSignal)||(NULL == inFilter)||(NULL == outConv))
return;
int n,k,kmin,kmax,p;
if(0 == shapeId) // 对于MATLAB conv(...,'shape') -----full
{
*convLen = signalLen + filterLen - 1;
for (n = 0; n < *convLen; n++)
{
outConv[n] = 0;
kmin = (n >= filterLen - 1) ? n - (filterLen - 1) : 0;
kmax = (n < signalLen - 1) ? n : signalLen - 1;
for (k = kmin; k <= kmax; k++)
{
outConv[n] += inSignal[k] * inFilter[n - k];
}
}
}
else if(1 == shapeId) // 对于MATLAB conv(...,'shape') -----valid
{
*convLen = signalLen - filterLen + 1;
for (n = filterLen - 1; n < signalLen; n++)
{
p = n - filterLen + 1;
outConv[p] = 0;
kmin = (n >= filterLen - 1) ? n - (filterLen - 1) : 0;
kmax = (n < signalLen - 1) ? n : signalLen - 1;
for (k = kmin; k <= kmax; k++)
{
outConv[p] += inSignal[k] * inFilter[n - k];
}
}
}
else
return ;
}
/**
* @brief 小波变换之分解
* @param sourceData 源数据
* @param dataLen 源数据长度
* @param db 过滤器类型
* @param cA 分解后的近似部分序列-低频部分
* @param cD 分解后的细节部分序列-高频部分
* @return 正常则返回分解后序列的数据长度,错误则返回-1
*/
int Wavelet::Decomposition(double* sourceData, int dataLen, Filter db, double* cA, double* cD)
{
if(dataLen < 2)
return -1;
if((NULL == sourceData)||(NULL == cA)||(NULL == cD))
return -1;
m_db = db;
int filterLen = m_db.length;
int i, n;
int decLen = (dataLen+filterLen-1)/2;
int convLen = 0;
double extendData[dataLen+2*filterLen-2];
double convDataLow[dataLen+filterLen-1];
double convDataHigh[dataLen+filterLen-1];
/*
MATLAB上dwt函数的工作过程
假设x=[x(1) x(2) x(3) x(4) x(5) x(6) x(7)],计算y=dwt(x,’db2’)。
其计算过程主要由两个部分组成:
1:边缘延拓,它主要由函数wextend完成。
2:卷积运算,它主要由函数conv2完成。
先看第一部分,仔细分析子程序部分,函数wextend的用法为y=wextend('1D','sym',x,3);
这样得到的y=[ x(3) x(2) x(1) x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(7) x(6) x(5)]
在看第二部分,仔细分析子程序部分,核心语句有z=conv2(y,Lo_D,'valid');
这里设Lo_D=[h(1) h(2) h(3) h(4)]。
3:最后就是下采样,其下采样是按照式a = z(2:2:length(z))进行的,高频低频部分均如此,项数为floor((7+4-1)/2)。
*/
// 1.边缘延拓
SignalExtension(0, 0 , sourceData, dataLen, filterLen, extendData);
// 2.卷积运算
Conv1(1, extendData, dataLen+2*filterLen-2, db.lowFilterDec, filterLen, convDataLow, &convLen);
Conv1(1, extendData, dataLen+2*filterLen-2, db.highFilterDec, filterLen, convDataHigh, &convLen);
// 3.下采样
Downsampling(convDataLow, dataLen + filterLen - 1, cA);
Downsampling(convDataHigh, dataLen + filterLen - 1, cD);
return decLen;
}
/**
* @brief 小波变换之重构
* @param cA 分解后的近似部分序列-低频部分
* @param cD 分解后的细节部分序列-高频部分
* @param cALength 输入数据长度
* @param RecLength 输入重构后的原始数据长度
* @param db 过滤器类型
* @param recData 重构后输出的数据
* @return 正常则返回重构数据长度,错误则返回-1
*/
int Wavelet::Reconstruction(double *cA, double *cD, int cALength, int RecLength, Filter db, double* recData)
{
if((NULL == cA)||(NULL == cD)||(NULL == recData))
return -1;
m_db = db;
int filterLen = m_db.length;
int i,j;
int n,k,p;
int recLen = RecLength;
int convLen = 0;
double convDataLow[recLen+filterLen-1];
double convDataHigh[recLen+filterLen-1];
double cATemp[2*cALength];
double cDTemp[2*cALength];
memset(convDataLow, 0, (recLen+filterLen-1)*sizeof(double)); // 清0
memset(convDataHigh, 0, (recLen+filterLen-1)*sizeof(double)); // 清0
memset(cATemp, 0, 2*cALength*sizeof(double)); // 清0
memset(cDTemp, 0, 2*cALength*sizeof(double)); // 清0
// 1.隔点插0
Upsampling(cA, cALength, cATemp);
Upsampling(cD, cALength, cDTemp);
// 2.卷积运算
Conv1(0, cATemp, 2*cALength-1, db.lowFilterRec, filterLen ,convDataLow, &convLen);
convLen = 0;
Conv1(0, cDTemp, 2*cALength-1, db.highFilterRec, filterLen ,convDataHigh, &convLen);
// 3.抽取结果及求和——实现类似MATLAB中的wkeep1(s,len,'c')的功能
k = (convLen - recLen)/2;
for(i=0; i<recLen; i++)
{
recData[i] = convDataLow[i + k] + convDataHigh[i + k];
}
return recLen;
}
|